ダイクストラ。
今までコード 1. のように書いてきたけど、コード 2. のようにループ前にコストを比較するようにしたり、コード 3. のように seen 配列を使うようにすると、ランダムなグラフで速くなった。
ダイクストラの実装はバリエーションが多く、速度差に影響するものもあるので、自分の実装を見直すのは良いかもしれない。

コード 1.

#include <iostream>
#include <algorithm>
#include <queue>
#include <tuple>
using namespace std;

struct edge { int to, cost; };

int main(void) {
  constexpr int inf = 987654321;
  int n, m; scanf("%d%d", &n, &m);
  vector<vector<edge>> G(n, vector<edge>());
  for(int i=0; i<m; ++i) {
    int a, b, c; scanf("%d%d%d", &a, &b, &c);
    G[a].push_back(edge{b, c});
    G[b].push_back(edge{a, c});
  }
  vector<int> cost(n, inf);
  cost[0] = 0;
  priority_queue<pair<int, int>, vector<pair<int, int>>, greater<pair<int, int>>> pq;
  // コスト、点番号
  pq.emplace(0, 0);
  while(!pq.empty()) {
    int _, v; tie(_, v) = pq.top(); pq.pop();
    for(edge e : G[v]) {
      if(cost[e.to] > cost[v] + e.cost) {
        cost[e.to] = cost[v] + e.cost;
        pq.emplace(cost[e.to], e.to);
      }
    }
  }
  int res = cost[n-1];
  if(res == inf) { res = -1; }
  printf("%d\n", res);
  return 0;
}
      

コード 2.

#include <iostream>
#include <algorithm>
#include <queue>
#include <tuple>
using namespace std;

struct edge { int to, cost; };

int main(void) {
  constexpr int inf = 987654321;
  int n, m; scanf("%d%d", &n, &m);
  vector<vector<edge>> G(n, vector<edge>());
  for(int i=0; i<m; ++i) {
    int a, b, c; scanf("%d%d%d", &a, &b, &c);
    G[a].push_back(edge{b, c});
    G[b].push_back(edge{a, c});
  }
  vector<int> cost(n, inf);
  cost[0] = 0;
  priority_queue<pair<int, int>, vector<pair<int, int>>, greater<pair<int, int>>> pq;
  // コスト、点番号
  pq.emplace(0, 0);
  while(!pq.empty()) {
    int c, v; tie(c, v) = pq.top(); pq.pop();
    if(cost[v] < c) { continue; }          // ここを足しました。
    for(edge e : G[v]) {
      if(cost[e.to] > cost[v] + e.cost) {
        cost[e.to] = cost[v] + e.cost;
        pq.emplace(cost[e.to], e.to);
      }
    }
  }
  int res = cost[n-1];
  if(res == inf) { res = -1; }
  printf("%d\n", res);
  return 0;
}
      

コード 3.

#include <iostream>
#include <algorithm>
#include <queue>
#include <tuple>
using namespace std;

struct edge { int to, cost; };

int main(void) {
  constexpr int inf = 987654321;
  int n, m; scanf("%d%d", &n, &m);
  vector<vector<edge>> G(n, vector<edge>());
  for(int i=0; i<m; ++i) {
    int a, b, c; scanf("%d%d%d", &a, &b, &c);
    G[a].push_back(edge{b, c});
    G[b].push_back(edge{a, c});
  }
  vector<int> cost(n, inf);
  cost[0] = 0;
  vector<bool> seen(n);                    // この
  priority_queue<pair<int, int>, vector<pair<int, int>>, greater<pair<int, int>>> pq;
  // コスト、点番号
  pq.emplace(0, 0);
  while(!pq.empty()) {
    int _, v; tie(_, v) = pq.top(); pq.pop();
    if(seen[v]) { continue; }              // 3行を
    seen[v] = true;                        // 足しました。
    for(edge e : G[v]) {
      if(cost[e.to] > cost[v] + e.cost) {
        cost[e.to] = cost[v] + e.cost;
        pq.emplace(cost[e.to], e.to);
      }
    }
  }
  int res = cost[n-1];
  if(res == inf) { res = -1; }
  printf("%d\n", res);
  return 0;
}
      

コード1. の場合:
キューの優先度がおかしいだけなので誤った答えを出すわけではないが、無駄な処理が増えるため遅くなる。
極端に遅くなる例として、以下のようなグラフが考えられる。

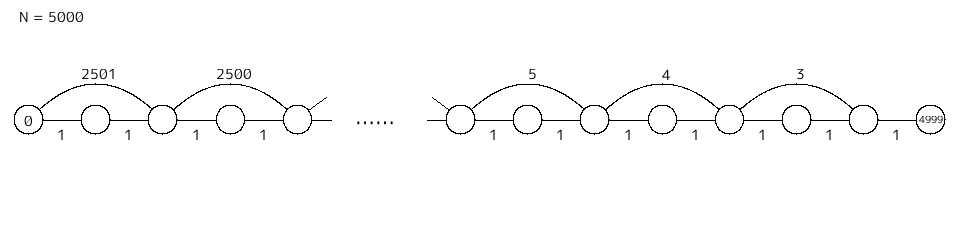
#!/usr/bin/python2
# -*- coding: utf-8 -*-
# †
N = 5000
arr = []
for i in xrange(N-1):
    arr.append([i, i+1, 1])
val = 3
for i in reversed(xrange(0, N-2, 2)):
    arr.append([i, i+2, val])
    val += 1

M = len(arr)
print N, M
for a, b, c in arr:
    print a, b, c
      

コード2. の場合:
コード1 と同様に遅くなる。

コード3. の場合:
seen 配列の存在により、それぞれの頂点で最小(?)コストをどんどん確定していくため、速いが誤った答えを出す。
競プロ的にも、サンプルケースで誤った答えを出しやすくなるので、こっちの方がバグに気付きやすいかも？

(ΦωΦ)＜つづく