(ΦωΦ)＜グラフ理論対策講座

TopCoder SRM 704 Div2 Med "ConnectedComponentConstruction"

要素数 $n$ の配列が与えられます。配列の各要素は、連結しているノードの数を表しています。
各ノードは自分自身とは連結している、と見なします。
このような無向グラフをひとつ作って下さい。無理なときはそれを指摘してください。
・$1 \le n \le 50$
・$1 \le$ 各要素の値 $\le n$

連結さえしていればよく、連結しているノード同士で閉路を構成する必要はない（閉路であっても良い）。
連結しているノード同士は、配列の値が同じになる。
配列に連結しているノードの数（＝配列の値）が何個あるかを数えたとき、
その個数は連結しているノードの数（＝配列の値）の倍数であればいい。等しくなくてもいい。

例えば、

[2, 2, 2, 2, 2, 2]

や

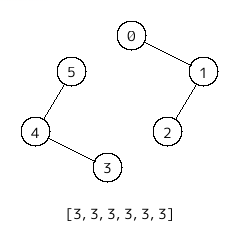
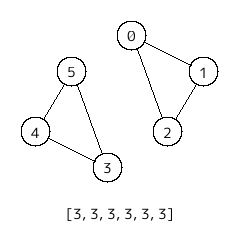
[3, 3, 3, 3, 3, 3]

のときは、2 が 6 個、3 が 6 個で、6 は 2 の倍数、6 は 3 の倍数なので以下のようにグラフを作ることができる。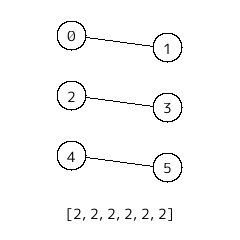

#include <iostream>
#include <algorithm>
using namespace std;

class ConnectedComponentConstruction { public: vector<string> construct(vector<int> s); };

vector<string> ConnectedComponentConstruction::
construct(vector<int> s) {
  int n = s.size();
  vector<string> G(n); // G[n]
  for(int i=0; i<n; ++i) {
    for(int j=0; j<n; ++j) { G[i] += 'N'; }
  }
  for(int size=2; size<=n; ++size) {
    vector<int> verts;
    for(int i=0; i<n; ++i) {
      if(s[i] == size) { verts.push_back(i); }
    }
    int m = verts.size();
    if(m % size != 0) { return vector<string>(); }
    for(int i=0; i<m; i+=size) {
      for(int j=i; j<i+size-1; ++j) {
        G[verts[j]][verts[j+1]] = 'Y';
        G[verts[j+1]][verts[j]] = 'Y';
      }
    }
  }
  return G;
}

---

補題

逆に、与えられたグラフに対して、連結しているノードの数をそれぞれのノードについて求めてください。
・$1 \le$ ノードの数 $\le 50$

サンプルケース
入力:

6
NYNYNN YNYNNN NYNYNN YNYNNN NNNNNY NNNNYN

出力:

4 4 4 4 2 2

三通りの解き方で求めてみよう。テストデータはこちら。

1. ワーシャルフロイド

#include <iostream>
#include <algorithm>
using namespace std;

vector<vector<bool>> G;

int main(void) {
  int n; scanf("%d", &n);
  G.assign(n, vector<bool>(n, false));
  for(int i=0; i<n; ++i) {
    string s; cin >> s;
    for(int j=0; j<n; ++j) {
      G[i][j] = s[j] == 'Y';
    }
    G[i][i] = true;
  }
  for(int k=0; k<n; ++k) {
    for(int i=0; i<n; ++i) {
      for(int j=0; j<n; ++j) {
        if(G[i][k] && G[k][j]) {
          G[i][j] = true;
        }
      }
    }
  }
  for(int i=0; i<n; ++i) {
    if(i) { putchar(' '); }
    int cnt = 0;
    for(int j=0; j<n; ++j) {
      if(G[i][j]) { ++cnt; }
    }
    printf("%d", cnt);
  }
  putchar('\n');
  return 0;
}

2. Union-Find

#include <iostream>
#include <algorithm>
using namespace std;

struct UnionFind {
  UnionFind(int);
  void unite(int, int);
  int find(int);
  int size_of(int);
  int size();
private:
  int n;
  vector<int> par;
};

UnionFind::UnionFind(int n) : par(n, -1), n(n) {}
void UnionFind::unite(int x, int y) {
  x = find(x), y = find(y);
  if(x == y) { return; }
  if(par[x] > par[y]) { swap(x, y); }
  par[x] += par[y];
  par[y] = x;
  --n;
}
int UnionFind::find(int x) { return par[x] < 0 ? x : par[x] = find(par[x]); }
int UnionFind::size_of(int x) { return -par[find(x)]; }
int UnionFind::size() { return n; }

int main(void) {
  int n; scanf("%d", &n);
  vector<string> G(n); // G[n]
  for(int i=0; i<n; ++i) { cin >> G[i]; }
  UnionFind uf(n);
  for(int i=0; i<n; ++i) {
    for(int j=i+1; j<n; ++j) {
      if(G[i][j] == 'Y') { uf.unite(i, j); }
    }
  }
  for(int i=0; i<n; ++i) {
    if(i) { putchar(' '); }
    printf("%d", uf.size_of(i));
  }
  putchar('\n');
  return 0;
}

3. 再帰

#include <iostream>
#include <algorithm>
using namespace std;

vector<string> G;
vector<int> root_of;

void rec(int par, int i) {
  root_of[i] = par;
  for(int j=0; j<par; ++j) {
    if(G[j][par] == 'Y') {
      rec(j, i);
      break; // この break は重要。無いと辺が多いときに遅くなる
    }
  }
}

int main(void) {
  int n; scanf("%d", &n);
  G.resize(n);
  for(int i=0; i<n; ++i) { cin >> G[i]; }
  root_of.assign(n, -1);
  for(int i=0; i<n; ++i) {
    if(root_of[i] == -1) { rec(i, i); }
  }
  for(int i=0; i<n; ++i) {
    if(i) { putchar(' '); }
    printf("%lu", count(begin(root_of), end(root_of), root_of[i]));
  }
  putchar('\n');
  return 0;
}

チャレンジできそうなテストケースの例:
・密グラフ、完全グラフ

(ΦωΦ)＜つづく