最初のサンプルを図示するとこうなる。

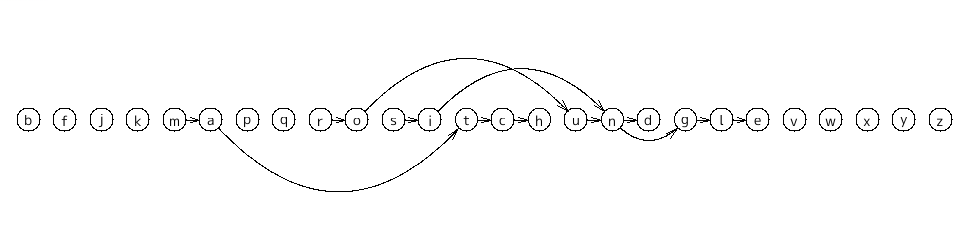
矢印の向きが同じ方向を向くようにすることができるかどうか、を判定すればいい。
つまり、アルファベット $26$ 文字のそれぞれをノードとする有向グラフで、
隣同士の文字が違うときに左の文字から右の文字へ辺を張り、
そのグラフがトポロジカルソートできるかどうかを調べることになる。

隣同士の文字が同じときに辺を張るとループを作っていることになるので、このときは辺を張ってはいけない。

グラフの問題だと見なすことができるかどうかが鍵になっているように思う。

#include <algorithm>
#include <queue>
using namespace std;

class AlphabetOrderDiv1 { public: string isOrdered(vector<string> words); };

bool topological_sort(const vector<vector<int>> &G, vector<int> &order) {
  const int n = G.size();
  vector<int> in_degrees(n, 0); // in_degrees[n]
  for(int i=0; i<n; ++i) {
    for(int to : G[i]) {
      ++in_degrees[to];
    }
  }
  queue<int> que;
  for(int i=0; i<n; ++i) {
    if(in_degrees[i] == 0) { que.push(i); }
  }
  order.assign(n, -1);
  int ptr = 0;
  while(!que.empty()) {
    int v = que.front(); que.pop();
    order[ptr++] = v;
    for(int u : G[v]) {
      if(--in_degrees[u] == 0) { que.push(u); }
    }
  }
  return ptr == n;
}

string AlphabetOrderDiv1::
isOrdered(vector<string> words) {
  int n = words.size();
  vector<vector<int>> G(26);
  for(int i=0; i<n; ++i) {
    string s = words[i];
    for(int j=0, m=s.size(); j<m-1; ++j) {
      int u = s[j]   - 'a',
          v = s[j+1] - 'a';
      if(u != v) { G[u].push_back(v); }
    }
  }
  vector<int> order;
  bool able = topological_sort(G, order);
  return able ? "Possible" : "Impossible";
}
      

(ΦωΦ)＜つづく