これ、なんかムズない??
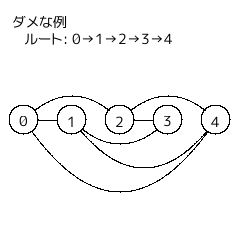
このようなときはダメらしい。深さ優先なら $1$ 番の次に $3$ 番に行けるでしょ、ということみたい。


ルートが番号の昇順になるように、まずはノード番号の貼り替えを行う。
すると、深さ優先探索で次に行くことになるノードは、番号の小さいものと決め打つことができるので、隣接リストをソートすることができる。
新たに来たノードでは訪問済みのフラグ立てを行い、本当に来るべきノードであったかを確認してからさらに深く辿る。最後まで行けたなら成功。

#include <iostream>
#include <algorithm>
#include <vector>
using namespace std;

int n, m;
vector<vector<int>> G;
vector<bool> seen;
int ptr; // 次に訪問したいノードの番号

// ノード v に来た
void rec(int v) {
  seen[v] = true;
  if(ptr != v) { return; } // 失敗
  if(++ptr == n) { return; } // 成功
  for(int u : G[v]) {
    if(!seen[u]) {
      rec(u);
    }
  }
}

int main(void) {
  scanf("%d%d", &n, &m);
  G.assign(n, vector<int>());
  seen.assign(n, false);
  vector<int> H(n);
  for(int i=0; i<n; ++i) {
    int x; scanf("%d", &x);
    H[--x] = i;
  }
  for(int i=0; i<m; ++i) {
    int a, b; scanf("%d%d", &a, &b);
    --a, --b;
    G[H[a]].push_back(H[b]);
    G[H[b]].push_back(H[a]);
  }
  for(int v=0; v<n; ++v) {
    sort(begin(G[v]), end(G[v]));
  }
  ptr = 0;
  rec(0);
  printf("%d\n", int(ptr == n));
  return 0;
}
      

(ΦωΦ)＜つづく