$\displaystyle \binom{n}{k}$ は ${}_n \mathrm{C}_k$ と同じです。

解説の
$\displaystyle \binom{n}{3} - \frac{\displaystyle \sum_{v} \binom{\mathrm{inDegree}(v)}{2} + \binom{\mathrm{outDegree}(v)}{2}}{2}$
の意味が分からんかった。
$\displaystyle \binom{n}{3} - \frac{\displaystyle \sum_{v} \binom{\mathrm{inDegree}(v)}{2} + \sum_{v} \binom{\mathrm{outDegree}(v)}{2}}{2}$
とする必要があるんじゃないかと悩んだりとか、同じもん足して $2$ で割るんだったら別に
$\displaystyle \binom{n}{3} - \sum_{v} \binom{\mathrm{inDegree}(v)}{2}$
でいいんじゃねーの、と思ったりとか。
もしこれで良いんだとしても、解説が何言ってるか分からんので理解できん。何語やねんアレ。文字が 26 種類しかないぞ。

最後の式で良い気がするので、これを考えてみる。
長さ $3$ の閉路の個数を求める方法として、任意の $3$ 頂点の組み合わせパターン数全体から「閉路になっていないもの」を減らす、というのはさすがに理解できる。

頂点数が $n$ のとき、ひとつの頂点 $v$ に注目すると次数（=入次数 + 出次数）は $n-1$ である。
長さ $3$ の閉路を作ろうとすると、それらから $2$ 本の辺を使うことになるが、入ってくる辺同士を組み合わせても閉路にはできない。
したがって頂点 $v$ において、長さ $3$ の閉路ができないパターン数は $\displaystyle \binom{\mathrm{inDegree}(v)}{2}$ になる。

逆に、頂点 $v$ において入ってくる辺ひとつと出ていく辺ひとつをペアにしたものをなるべく多く作ることができれば、閉路数を最大化できる。
つまり、$v$ の入次数と出次数が極力近ければ良い。
答えは条件さえ満たせば何でもいいので、簡単なものにしたいと考えると '0' と '1' を交互に出力すればいい。
'0' から始めようが '1' から始めようが、どっちでも問題ない。

ちなみに、長さ $4$ の閉路の数え方を考えたとき、同じ方法ではできない。
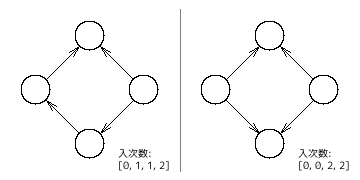
これは頂点数 $4$ で閉路になっていないような入次数の組み合わせが次のようになり、閉路にできない条件が一意に決まらないからである。

#include <iostream>
#include <algorithm>
#include <vector>
using namespace std;
using i64 = long long;

// 与えられたグラフから、長さ3の閉路の個数を数える。
i64 count(vector<vector<bool>> &G) {
  i64 n = G.size();
  i64 res = n * (n-1) * (n-2) / 6;
  for(int i=0; i<n; ++i) {
    i64 indeg = 0;
    for(int j=0; j<n; ++j) {
      if(i == j) { continue; }
      if(G[i][j]) { ++indeg; }
    }
    res -= indeg * (indeg-1) / 2;
  }
  return res;
}

int main(void) {
  i64 n; scanf("%lld", &n);
  vector<vector<bool>> G(n, vector<bool>(n, false)); // G[n][n]
  for(int i=0, flag=0; i<n; ++i) {
    for(int j=i+1; j<n; ++j) {
      if(flag) { G[i][j] = true; }
      else     { G[j][i] = true; }
      flag = !flag;
    }
  }
  i64 cnt = count(G);
  printf("%lld\n", cnt);
  for(int i=0; i<n; ++i) {
    for(int j=i+1; j<n; ++j) {
      putchar('0' + G[i][j]);
    }
  }
  putchar('\n');
  return 0;
}
      

コマンドライン引数からのファイル入力でテストケースを受けとり、標準入力で答案の出力を受けとることにする。

#include <iostream>
#include <algorithm>
#include <vector>
#include <fstream>
#include <cassert>
using namespace std;
using i64 = long long;

// 最大数はこういう求め方もあるみたい。
// i64 calc(i64 n) {
//   if(n & 1) { return n * (n*n-1) / 24; }
//   return n * (n*n-4) / 24;
// }

// 与えられたグラフから、長さ3の閉路の個数を数える。
i64 count(vector<vector<bool>> &G) {
  i64 n = G.size();
  i64 res = n * (n-1) * (n-2) / 6;
  for(int i=0; i<n; ++i) {
    i64 indeg = 0;
    for(int j=0; j<n; ++j) {
      if(i == j) { continue; }
      if(G[i][j]) { ++indeg; }
    }
    res -= indeg * (indeg-1) / 2;
  }
  return res;
}

int main(int argc, char **argv) {
  ifstream infle(argv[1], ios_base::in);
  string s; getline(infle, s);
  i64 n = stoll(s);
  vector<vector<bool>> G(n, vector<bool>(n, false)); // G[n][n]
  // 個数が最大になるようなグラフを構築して…
  for(int i=0, flag=false; i<n; ++i) {
    for(int j=i+1; j<n; ++j) {
      if(flag) { G[i][j] = true; }
      else     { G[j][i] = true; }
      flag = !flag;
    }
  }
  // 個数を求める。
  i64 ans = count(G);

  // ここから答案の答え合わせ
  i64 cnt; scanf("%lld", &cnt);
  fprintf(stderr, "cnt =%lld, ans=%lld\n", cnt, ans);
  assert(cnt == ans);
  cin >> s;
  assert(s.size() == n * (n-1) / 2);
  G.assign(n, vector<bool>(n, false));
  // 答案のグラフを構築して…
  for(int i=0, ptr=0; i<n; ++i) {
    for(int j=i+1; j<n; ++j) {
      if(s[ptr++] == '1') { G[i][j] = true; }
      else                { G[j][i] = true; }
    }
  }
  // 個数を求める。
  i64 cnt2 = count(G);
  fprintf(stderr, "cnt2=%lld, ans=%lld\n", cnt2, ans);
  assert(cnt2 == ans);

  return 0;
}
      

(ΦωΦ)＜つづく