トーナメントグラフのネタがカブった。

ここでは、フローを流すことによって条件を満たすようなグラフを構築する方法を考える。
頂点数が $n$ のとき、辺は $\displaystyle \frac{n(n-1)}{2}$ 本あるはずで、
それらの頂点や辺を状態（＝フローを流すグラフのノード）とする。


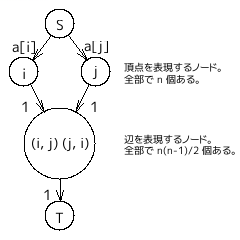
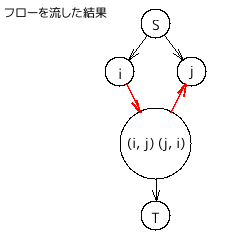
$\displaystyle \frac{n(n-1)}{2}$ 本の辺それぞれに向かってその辺が繋いでいる二頂点からフローを流したとき、
一方から流入しているときには他方へは流出しているはずで（上右図の赤矢印）、
この情報から、条件を満たすようなグラフを構築することができる。
グラフが構築できれば、ワーシャルフロイドなどで到達できる頂点を調べて、それらを数えればいい。

以下の実装では、頂点を表現するノードを $0$ 番から、辺を表現するノードを $n$ 番から採番している。
最後のふたつがソースとシンクである。

#include <iostream>
#include <algorithm>
using namespace std;

class ScoresSequence { public: int count(vector<int> a); };

constexpr int inf = 987654321;

struct Edge {
  int dst, rev;
  int cap;
};

int size;
vector<bool> used;
vector<vector<Edge>> g;
vector<vector<int>> edge;
vector<int> path;

void init_graph(int size) {
  ::size = size;
  g.assign(size, vector<Edge>());
}

void add_edge(int src, int dst, int cap) {
  g[src].push_back(Edge({dst, int(g[dst].size()),   cap}));
  g[dst].push_back(Edge({src, int(g[src].size())-1, 0}));
}

int dfs(int u, int t, int flow) {
  if(u == t) { return flow; }
  used[u] = true;
  for(Edge &e : g[u]) {
    if(used[e.dst]) { continue; }
    if(e.cap <= 0)  { continue; }
    int fl = dfs(e.dst, t, min(flow, e.cap));
    if(fl == 0) { continue; }
    e.cap -= fl;
    g[e.dst][e.rev].cap += fl;
    return fl;
  }
  return 0;
}

int max_flow(int s, int t) {
  for(int res=0; ; ) {
    used.assign(size, false);
    int flow = dfs(s, t, inf);
    if(flow == 0) { return res; }
    res += flow;
  }
}

int ScoresSequence::
count(vector<int> a) {
  int n = a.size();
  int cnt = 1 + n + n*(n-1)/2 + 1;
  int src = cnt - 2, dst = cnt - 1;
  init_graph(cnt);
  for(int i=0, ptr=n; i<n; ++i) {
    add_edge(src, i, a[i]);
    for(int j=i+1; j<n; ++j) {
      add_edge(i, ptr, 1);
      add_edge(j, ptr, 1);
      add_edge(ptr, dst, 1);
      ++ptr;
    }
  }
  max_flow(src, dst);
  vector<vector<bool>> G(n, vector<bool>(n, false));
  for(int i=0; i<n; ++i) { G[i][i] = true; }
  for(int k=n; k<cnt-2; ++k) {
    for(Edge e : g[k]) {
      if(e.cap && 0 <= e.rev && e.rev < n && 0 <= e.dst && e.dst < n) { G[e.rev][e.dst] = true; }
    }
  }
  for(int k=0; k<n; ++k) {
    for(int i=0; i<n; ++i) {
      for(int j=0; j<n; ++j) {
        if(G[i][k] && G[k][j]) {
          G[i][j] = true;
        }
      }
    }
  }
  int res = 0;
  for(int i=0; i<n; ++i) {
    for(int j=0; j<n; ++j) {
      res += G[i][j];
    }
  }
  return res;
}
      

(ΦωΦ)＜つづく