$n$ 棟の建物があり、それらは全て $k$ 階建てです。
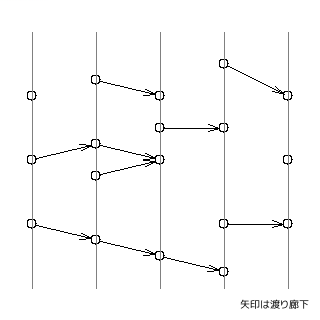
$m$ 個の渡り廊下があり、それぞれ 第 $a_{i}$ 棟の $b_{i}$ 階から第 $a_{i}+1$ 棟の $c_{i}$ 階への一方通行になっています。
第 $0$ 棟の $s$ 階から第 $n-1$ 棟の $t$ 階までの階段の昇降回数を最小化したいとき、その最小値を求めてください。
・$1 \le n \le 2 \times 10^{5}$
・$0 \le m \le 2 \times 10^{5}$
・$1 \le k \le 10^{9}$
ライターの解説は準備中とあるが、もう望み薄だろう。
ライターの答案も見てはみたが、理解できなかった。
ライターの答案もテスターの答案もユニークなように見える。
---
渡り廊下のある階だけを経由していけば良いだろう、というのは分かる。
渡り廊下のある階は最大で $2m$ 個あるので、
それらに加えてスタート(第 $0$ 棟 $s$ 階)とゴール(第 $n-1$ 棟 $t$ 階)を含めた階を頂点とするグラフを作り、ダイクストラをしたい。
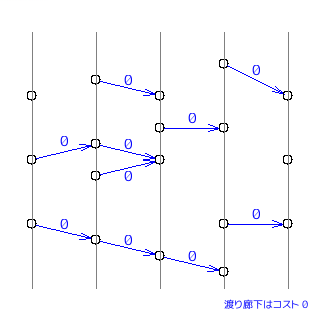
渡り廊下の始点となる第 $a_{i}$ 棟の $b_{i}$ 階から、終点となる第 $a_{i}+1$ 棟の $c_{i}$ 階へコスト $0$ の辺を張る。
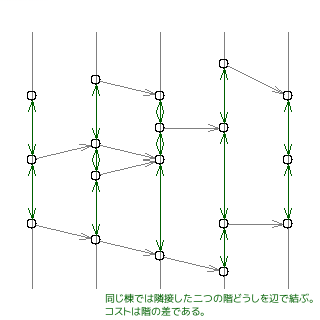
同じ棟どうしは階段で昇降できるが、任意の二頂点に辺を張ると量が多いので、隣り合った二頂点だけに辺を張るようにする。
もし、ある棟に頂点が $x$ 個あったとしたら、全てに辺を張ると $x(x-1)$ 本になってしまうが、
隣り合った二頂点にだけ辺を張るようにすると、$2(x-1)$ 本で済み、それで充分である。
#include <iostream>
#include <algorithm>
#include <map>
#include <queue>
using namespace std;
using i64 = long long;
struct edge { int to; i64 cost; };
int main(void) {
constexpr i64 inf = 987654321987654321LL;
int n, m, k, s, t; scanf("%d%d%d%d%d", &n, &m, &k, &s, &t);
--s, --t;
int N = 0; // 頂点数
vector<map<int, int>> mp(n); // 座標圧縮用データ。 mp[a][b] := a棟b階についた連番
vector<vector<int>> route(n); // route[a] := a棟からa+1棟へ廊下がある階のリスト
vector<tuple<int, int, int>> dat; // 入力で与えられる m 個の渡り廊下のリスト
mp[0] [s] = N++;
mp[n-1][t] = N++;
route[0] .push_back(s);
route[n-1].push_back(t);
for(int i=0; i<m; ++i) {
int a, b, c; scanf("%d%d%d", &a, &b, &c);
--a, --b, --c;
dat.emplace_back(a, b, c);
if(!mp[a].count(b)) {
mp[a][b] = N++;
route[a].push_back(b);
}
if(!mp[a+1].count(c)) {
mp[a+1][c] = N++;
route[a+1].push_back(c);
}
}
vector<vector<edge>> G(N);
for(int i=0; i<m; ++i) {
int a, b, c; tie(a, b, c) = dat[i];
G[mp[a][b]].push_back(edge{mp[a+1][c], 0});
}
for(int a=0; a<n; ++a) {
sort(begin(route[a]), end(route[a]));
for(int k=0, size=route[a].size(); k<size-1; ++k) {
int b0 = route[a][k],
b1 = route[a][k+1];
if(b0 == b1) { continue; }
int u = mp[a][b0],
v = mp[a][b1];
G[u].push_back(edge{v, b1-b0});
G[v].push_back(edge{u, b1-b0});
}
}
// ここからダイクストラ
vector<i64> cost(N, inf);
vector<bool> seen(N, false);
cost[mp[0][s]] = 0;
priority_queue<pair<i64, int>, vector<pair<i64, int>>, greater<pair<i64, int>>> pq;
// コスト、点番号
pq.emplace(0, mp[0][s]);
while(!pq.empty()) {
i64 _; int v; tie(_, v) = pq.top(); pq.pop();
if(seen[v]) { continue; }
seen[v] = true;
for(edge e : G[v]) {
if(cost[e.to] > cost[v] + e.cost) {
cost[e.to] = cost[v] + e.cost;
pq.emplace(cost[e.to], e.to);
}
}
}
i64 res = cost[mp[n-1][t]];
if(res == inf) { res = -1; }
printf("%lld\n", res);
return 0;
}
参考: #223337
(ΦωΦ)<おしまい


