(ΦωΦ)＜yukicoder No.618「labo-index」

初期状態が空の配列に対し、$Q$ 回のクエリが来ます。毎回のクエリは次の三種類のいずれかです。

[追加] 値 $x$ が加わる。
[削除] $i$ 番目め (1-indexed) に加わった値を消す。
[バフ] 配列の値を全て $+x$ する。

各クエリ処理ごとに「値が $l$ 以上である要素が $l$ 個以上存在する」という条件を満たす最大の非負整数を求めてください。

・$1 \le Q \le 10^{5}$
・1番または3番のクエリのとき、$-10^{9} \le x \le 10^{9}$
・2番のクエリのとき、$i \ge 1$ かつ、この番号の値が配列に存在していることは保証される。

[バフ] は実際には [全体バフ] であり、更には [全体デバフ] である可能性もありますが、無理矢理 [バフ] と呼びます。

---
まず、セグメントツリーで範囲の最大値を記憶させる方法が思いついた。
以下の例を考える。

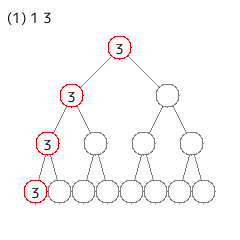
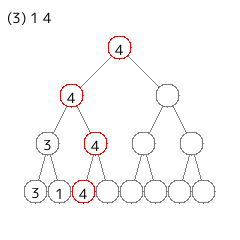
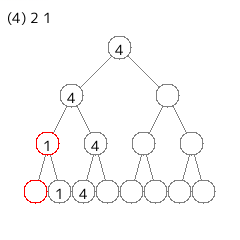
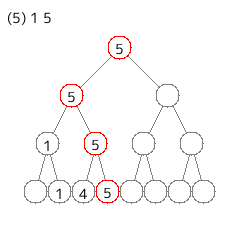
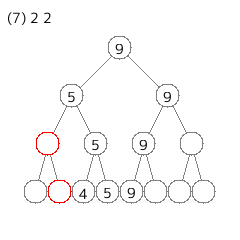
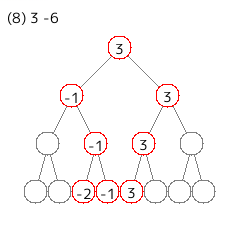
[追加] や [削除] は速くできそうだが、[バフ] は要素のある葉を全部更新しないといけないので、しんどそうである。
ここで、[バフ] では全ての要素が同じ値だけ上下することに注意すると、
ツリーの値を編集するのではなく、条件の部分のボーダーを変更することで対処できるのではないか、という判断ができる。

上記の例で考えてみる。
(7) のクエリの後、題意を満たす値を求める。答えは 3 である。

条件	真偽	解説
値が 0 以上である要素が 0 個以上存在する	O	4, 5, 9 の 3 個
値が 1 以上である要素が 1 個以上存在する	O	〃
値が 2 以上である要素が 2 個以上存在する	O	〃
値が 3 以上である要素が 3 個以上存在する	O	〃
値が 4 以上である要素が 4 個以上存在する	X	〃
値が 5 以上である要素が 5 個以上存在する	X	5, 9 の 2 個

そして (8) のクエリの後のことを、(7) のグラフで考える。
全体が -6 されたので、ボーダーが 6 上がったと考える。答えは 1 である。

条件	真偽	解説
値が 6 以上である要素が 0 個以上存在する	O	9 が 1 個
値が 7 以上である要素が 1 個以上存在する	O	〃
値が 8 以上である要素が 2 個以上存在する	X	〃
値が 9 以上である要素が 3 個以上存在する	X	〃
値が 10 以上である要素が 4 個以上存在する	X	なし
値が 11 以上である要素が 5 個以上存在する	X	〃

この後、9 回めのクエリとして、

1 5

というコマンドで 5 を追加することになったとする。
このとき、現状ではボーダーが 6 上がっているので、追加する数字にも 6 だけ下駄を履かせて、11 を追加すると考える必要がある。

---
肝心の「値が $l$ 以上である要素の個数」を数える部分であるが、
値と要素数には単調性があるので（要求する最小の値が大きくなれば要素数は減る）、値を二分法で決めて、それ以上の要素の個数を毎回数える方法が考えられる。

ただ、今回のようなセグメントツリーの構築方法だと、根から枝刈りしながら数える方法ぐらいしか考えられず、値によっては非常に時間がかかってしまう。
他の方法を考える必要がある。

ここまでの考え方を実装したコード (TLE)

#include <iostream>
#include <algorithm>
using namespace std;
using i64 = long long;

constexpr i64 inf = 987654321987654321LL;
constexpr i64 INIT = -inf;
int min_pow2, size;
vector<i64> tree; // セグメントツリー
i64 val;

// Q以上の最小の2の羃
int calc(int Q) {
  int res = 1;
  while(res < Q) { res *= 2; }
  return res;
}

void print_segtree() {
  fprintf(stderr, "=== print start ===\n");
  for(int i=1, lf=2; i<size; ++i) {
    if(tree[i] == INIT) { fprintf(stderr, "-"); }
    else                { fprintf(stderr, "%lld", tree[i]); }
    if(i+1 == lf) { fprintf(stderr, "\n"); lf *= 2; }
    else          { fprintf(stderr, " "); }
  }
  fprintf(stderr, "=== print  end  ===\n");
}

void update(int i, i64 x) {
  int pos = i + min_pow2;
  tree[pos] = x;
  pos /= 2;
  while(pos > 0) {
    tree[pos] = max(tree[pos*2], tree[pos*2+1]);
    pos /= 2;
  }
//  print_segtree();
}

// val以上の要素が pos番目の要素以下に 何個あるか数える
int rec(int pos) {
  if(min_pow2 <= pos && pos < size) {
    return tree[pos] >= val;
  }
  int res = 0;
  if(tree[pos] >= val) {
    res += rec(pos*2);
    res += rec(pos*2+1);
  }
  return res;
}

int main(void) {
  int Q; scanf("%d", &Q);
  min_pow2 = calc(Q);
  size = min_pow2 * 2;
  tree.assign(size, INIT);
  i64 border = 0;
  for(int i=0, ptr=0; i<Q; ++i) {
    int t; i64 x; scanf("%d%lld", &t, &x);
    switch(t) {
      case 1:
        update(ptr++, x+border);
        break;
      case 2:
        update(--x, INIT);
        break;
      case 3:
        border -= x;
        break;
    }
    i64 lo = -Q, hi = Q;
    while(hi - lo > 1) {
      i64 md  = (lo + hi) / 2;  // md: 研究力
      val = md + border;
      int cnt = rec(1); // cnt: 人数
      if(cnt >= md) {
        lo = md;
      } else {
        hi = md;
      }
    }
    printf("%lld\n", lo);
  }
  return 0;
}

===
もし、毎回のクエリ終了後に値がソートされていたとする。
上の例だと、次のようになる。

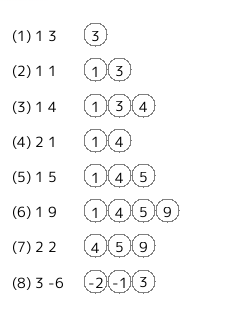
このとき、値 $l$ が条件を満たすのであれば、それは必ず後ろから $l$ 番目より前にあるべきであるということに気付かないといけない。
また、[バフ] に関しては、先に考えたボーダーをずらすという方法で対応する。

ただ、時間的に毎回ソートできない。
そこで、平衡二分探索木を実装し、そこに詰めていく方法を取ることにする。
実装としては Treap や RBST 等がある。ここでは RBST にする。

#include <iostream>
#include <vector>
using namespace std;
using i64 = long long;
using u32 = unsigned int;

u32 uy = time(NULL);
u32 xorshift32() {
  uy ^= uy << 14;
  uy ^= uy >> 13;
  uy ^= uy << 15;
  return uy;
}

template <typename T>
bool __attribute__((noinline)) is_null(T* obj) { return obj == nullptr; }

// RBST (Randomised Binary Search Tree)
template <class T>
struct RBST {
  struct Node { // {{{ Node
    constexpr static T nullval = -1; // valueAt() で不正な場所が指定されたときに返す値.
    T val;
    int treeSize;
    Node *lo, *hi;

    Node(T val) : val(val), treeSize(1), lo(nullptr), hi(nullptr) {}

    int size() {
      if(is_null(this)) { return 0; }
      return treeSize;
    }

    Node* update() {
      treeSize = lo->size() + hi->size() + 1;
      return this;
    }

    static Node* merge(Node *l, Node *r) {
      if(is_null(l)) { return r; }
      if(is_null(r)) { return l; }
      int lSize = l->size(),
          rSize = r->size();
      if(xorshift32() % (lSize + rSize) < lSize) {
        l->hi = merge(l->hi, r);
        return l->update();
      } else {
        r->lo = merge(l, r->lo);
        return r->update();
      }
    }

    pair<Node*, Node*> split(int k) { // [0, k), [k, n)
      if(is_null(this)) { return make_pair(nullptr, nullptr); }
      if(k <= lo->size()) {
        auto s = lo->split(k);
        lo = s.second;
        return make_pair(s.first, update());
      } else {
        auto s = hi->split(k - lo->size() - 1);
        hi = s.first;
        return make_pair(update(), s.second);
      }
    }

    int indexOf(T val) {
      if(is_null(this)) { return -1; }
      if(val == this->val) { return lo->size(); }
      if(val <  this->val) {
        return lo->indexOf(val);
      } else {
        return lo->size() + 1 + hi->indexOf(val);
      }
    }

    T valueAt(int pos) {
      if(is_null(this)) { return nullval; }
      int loSize = lo->size();
      if(loSize == pos) { return val; }
      if(loSize > pos) {
        return lo->valueAt(pos);
      } else {
        return hi->valueAt(pos - lo->size() - 1);
      }
    }

    int lowerBound(T val) {
      if(is_null(this)) { return 0; }
      if(val <= this->val) { return lo->lowerBound(val); }
      return hi->lowerBound(val) + lo->size() + 1;
    }

    int upperBound(T val) {
      if(is_null(this)) { return 0; }
      if(val >= this->val) { return lo->size() + 1 + hi->upperBound(val); }
      return lo->upperBound(val);
    }

    int count(T val) {
      return upperBound(val) - lowerBound(val);
    }

    Node* insert(int pos, T val) {
      Node *p = new Node(val);
      auto s = split(pos);
      return merge(merge(s.first, p), s.second);
    }

    Node* insert(T val) {
      return insert(lowerBound(val), val);
    }

    Node* deleteAt(int pos) {
      auto s = split(pos);
      auto t = s.second->split(1);
      t.first = nullptr;
      return merge(s.first, t.second);
    }

    void dump(int x) {
      if(is_null(this)) { return; }
      fprintf(stderr, "%c", "([{"[x%3]);
      lo->dump(x+1);
      fprintf(stderr, "%d", val);
      hi->dump(x+1);
      fprintf(stderr, "%c", ")]}"[x%3]);
    }
  }; // }}}
  Node *root;
  RBST() { root = nullptr; }
  int size() { return root->size(); }
  int indexOf(T val) { return root->indexOf(val); }
  T valueAt(int pos) { return root->valueAt(pos); }
  int lowerBound(T val) { return root->lowerBound(val); }
  int upperBound(T val) { return root->upperBound(val); }
  int count(T val) { return root->count(val); }
  void insert(T val) { root = root->insert(val); }
  void deleteAt(int pos) { root = root->deleteAt(pos); }
  void deleteValue(T val) { deleteAt(indexOf(val)); }
  void dump() { root->dump(0); fprintf(stderr, "\n"); }
};

int main(void) {
  int Q; scanf("%d", &Q);
  i64 border = 0;
  RBST<i64> tree;
  vector<i64> memo;
  int t; i64 x;
  for(int i=0; i<Q; ++i) {
    scanf("%d%lld", &t, &x);
    if(t == 1) {
      memo.push_back(x + border);
      tree.insert(memo.back());
    } else if(t == 2) {
      tree.deleteValue(memo[--x]);
    } else {
      border -= x;
    }
    i64 lo = -Q, hi = Q;
    while(hi - lo > 1) {
      i64 md = (lo + hi) / 2;
      i64 val = md + border;
      if(tree.size() - tree.lowerBound(val) >= md) { // 値が val 以上の要素数を数える
        lo = md;
      } else {
        hi = md;
      }
    }
    printf("%lld\n", lo);
  }
  return 0;
}

(ΦωΦ)＜おしまい