(ΦωΦ)<グラフ理論 用語集
あたしがグラフをキライな理由のひとつに用語が独特すぎるというのがあるんです。独特すぎて覚えられないし、覚えても独特すぎてすぐ忘れる。
なので、ここでまとめておきます。
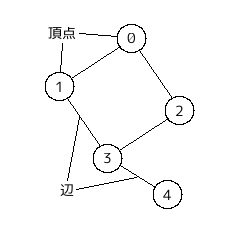
・頂点 (vertex, 複: vertices, vertexes)
右図参照。ノード(node) ということも。
・辺 (edge)
右図参照。
右図参照。ノード(node) ということも。
・辺 (edge)
右図参照。
・端点 (end point)
辺が接続する二つの頂点をその辺の端点という。
・次数 (degree, valency)
頂点に接合する辺の数。有向グラフのとき、入ってくる辺の数を入次数 (indegree)、出ていく辺の数を出次数 (outdegree) という。
・孤立点 (isolated vertex)
次数が $0$ の頂点。
・密グラフ (dense graph)
頂点の数に比べて辺の数が比較的多いグラフのこと。
・疎グラフ (sparse graph)
頂点の数に比べて辺の数が比較的少ないグラフのこと。
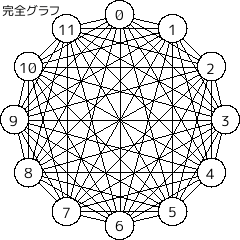
・完全グラフ (complete graph)
任意の二頂点間に辺があるグラフ。
辺が接続する二つの頂点をその辺の端点という。
・次数 (degree, valency)
頂点に接合する辺の数。有向グラフのとき、入ってくる辺の数を入次数 (indegree)、出ていく辺の数を出次数 (outdegree) という。
・孤立点 (isolated vertex)
次数が $0$ の頂点。
・密グラフ (dense graph)
頂点の数に比べて辺の数が比較的多いグラフのこと。
・疎グラフ (sparse graph)
頂点の数に比べて辺の数が比較的少ないグラフのこと。
・完全グラフ (complete graph)
任意の二頂点間に辺があるグラフ。
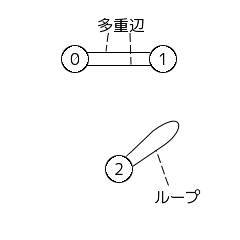
・多重辺 (multiple edges)
二頂点間に複数の辺がある場合の、その辺。
そもそも無いという前提であることも多いが、そうでない場合には、コストが最小/最大の辺のみを考えるなどの対応をすることもある。
・ループ (loop)
両端点が同じである辺。丁寧に自己ループといったりもする。
・単純グラフ (simple graph)
多重辺もループも含まないグラフのこと。
・部分グラフ (subgraph)
グラフ $G$ と $H$ について、$H$ の頂点集合と辺集合が共に $G$ の頂点集合と辺集合の部分集合となっているとき、
$H$ は $G$ の部分グラフであるという。逆に $G$ は $H$ の拡大グラフであるという。
二頂点間に複数の辺がある場合の、その辺。
そもそも無いという前提であることも多いが、そうでない場合には、コストが最小/最大の辺のみを考えるなどの対応をすることもある。
・ループ (loop)
両端点が同じである辺。丁寧に自己ループといったりもする。
・単純グラフ (simple graph)
多重辺もループも含まないグラフのこと。
・部分グラフ (subgraph)
グラフ $G$ と $H$ について、$H$ の頂点集合と辺集合が共に $G$ の頂点集合と辺集合の部分集合となっているとき、
$H$ は $G$ の部分グラフであるという。逆に $G$ は $H$ の拡大グラフであるという。
・道、パス (path)
グラフから任意の頂点を取り出して並べ、その隣接2頂点間の全てで辺が存在するとき、始点から終点までの辺の集まりを道という。
選んだ頂点は同じものが重複していても良い。
$v_{0}, v_{1}, \cdots, v_{n} \in V \Leftrightarrow \{v_{0}, v_{1}\}, \{v_{1}, v_{2}\}, \cdots, \{v_{n-1}, v_{n}\} \in E$
・単純道、単純パス (simple path)
同じ頂点が重複しない道。
流儀によっては、これを "道" と呼び、頂点が重複することを認めるものを歩道 (walk) と呼ぶこともある。
この流儀では歩道から辺の重複を取り除いたものは小径 (trail) という (Bondy and Murty 1976)。
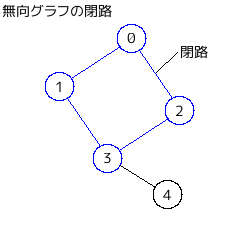
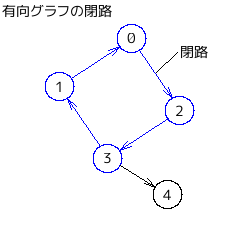
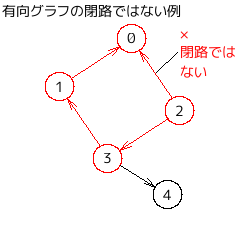
・閉路 (cycle)
始点と終点が同じ頂点である道。
ループと間違えやすいし、実際、閉路のことをループと表現しているプログラムや文章もわりと見かけるので、
書くときには間違えないように、読むときには騙されないようにすること。
・単純閉路 (simple cycle)
始点/終点以外の頂点が重複していない閉路。
・ハミルトン閉路 (Hamiltonian cycle)
グラフの全ての頂点を含む単純閉路。全ての頂点を一度だけ辿る。
※道と表現してあるが意味合いは単純道、閉路と表現してあるが意味合いは単純閉路であることも多い。
グラフから任意の頂点を取り出して並べ、その隣接2頂点間の全てで辺が存在するとき、始点から終点までの辺の集まりを道という。
選んだ頂点は同じものが重複していても良い。
$v_{0}, v_{1}, \cdots, v_{n} \in V \Leftrightarrow \{v_{0}, v_{1}\}, \{v_{1}, v_{2}\}, \cdots, \{v_{n-1}, v_{n}\} \in E$
・単純道、単純パス (simple path)
同じ頂点が重複しない道。
流儀によっては、これを "道" と呼び、頂点が重複することを認めるものを歩道 (walk) と呼ぶこともある。
この流儀では歩道から辺の重複を取り除いたものは小径 (trail) という (Bondy and Murty 1976)。
・閉路 (cycle)
始点と終点が同じ頂点である道。
ループと間違えやすいし、実際、閉路のことをループと表現しているプログラムや文章もわりと見かけるので、
書くときには間違えないように、読むときには騙されないようにすること。
・単純閉路 (simple cycle)
始点/終点以外の頂点が重複していない閉路。
・ハミルトン閉路 (Hamiltonian cycle)
グラフの全ての頂点を含む単純閉路。全ての頂点を一度だけ辿る。
※道と表現してあるが意味合いは単純道、閉路と表現してあるが意味合いは単純閉路であることも多い。
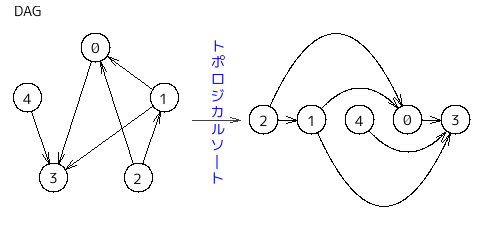
・DAG
Directed Acyclic Graph. 有向非巡回グラフ。
閉路がない有向グラフのこと。
DAG は必ずトポロジカルソートすることができる。
DAG をトポロジカルソートして DP というのは、定石のひとつ。
・トポロジカルソート (topological sort)
有向グラフにおいて、
ノードを一直線に並べたとき矢印の向きが全て同じ方向を向くように、ノードを並べること。
・トポロジカル順序 (topological order)
トポロジカルソートした結果、その順序をトポロジカル順序という。
Directed Acyclic Graph. 有向非巡回グラフ。
閉路がない有向グラフのこと。
DAG は必ずトポロジカルソートすることができる。
DAG をトポロジカルソートして DP というのは、定石のひとつ。
・トポロジカルソート (topological sort)
有向グラフにおいて、
ノードを一直線に並べたとき矢印の向きが全て同じ方向を向くように、ノードを並べること。
・トポロジカル順序 (topological order)
トポロジカルソートした結果、その順序をトポロジカル順序という。
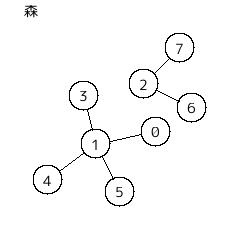
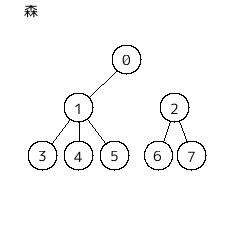
・森 (forest)
閉路を持たない(連結であるとは限らない)グラフを森という。
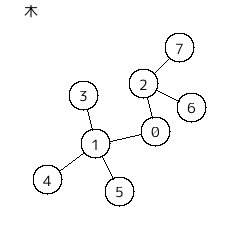
・木 (tree)
連結で閉路を持たないグラフを木という。木は森である。// (゚Д゚)ハァ?
また、森を "複数の木の集まり" と見なすこともできる。
木の特徴:
- 頂点が $n$ 個のとき、辺は $n-1$ 個である。
- 任意の二頂点間の道がちょうど一つある。
- 木に閉路はないが、新しい辺を一本加えると閉路が必ず一つできる。
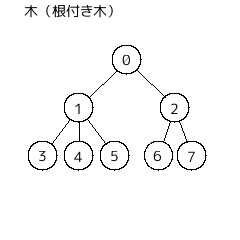
・根付き木 (rooted tree)
木には、
「あるノードを一番上に、そのノードから遠い頂点ほど下になるように配置することができる」
という特徴がある。このノードは木に必ずひとつだけ存在し、これを根 (root) という。
木をこのように配置したとき、根の存在を重視する目的で根付き木と呼ぶ。
辺をすべて下向きの矢印になるような有向辺にしたとき、以下のような特徴を持つ。
- 根は入次数 $0$ の頂点であり、ただひとつ存在する。
- 根以外の頂点の入次数は $1$ である。
- 各頂点には根からの有向道がひとつだけ存在する。
閉路を持たない(連結であるとは限らない)グラフを森という。
・木 (tree)
連結で閉路を持たないグラフを木という。木は森である。// (゚Д゚)ハァ?
また、森を "複数の木の集まり" と見なすこともできる。
木の特徴:
- 頂点が $n$ 個のとき、辺は $n-1$ 個である。
- 任意の二頂点間の道がちょうど一つある。
- 木に閉路はないが、新しい辺を一本加えると閉路が必ず一つできる。
・根付き木 (rooted tree)
木には、
「あるノードを一番上に、そのノードから遠い頂点ほど下になるように配置することができる」
という特徴がある。このノードは木に必ずひとつだけ存在し、これを根 (root) という。
木をこのように配置したとき、根の存在を重視する目的で根付き木と呼ぶ。
辺をすべて下向きの矢印になるような有向辺にしたとき、以下のような特徴を持つ。
- 根は入次数 $0$ の頂点であり、ただひとつ存在する。
- 根以外の頂点の入次数は $1$ である。
- 各頂点には根からの有向道がひとつだけ存在する。
・連結 (connected), 強連結 (strongly connected)
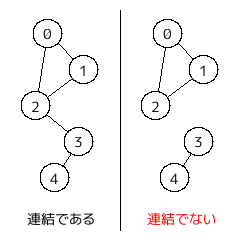
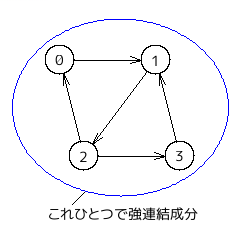
どの二頂点間にもパスがあるとき、グラフは連結であるという。
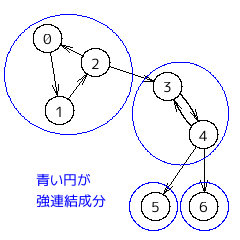
孤立点があればグラフは連結ではないことになるが、「孤立点が無ければグラフは連結である」は正しいとは限らない(右図参照)。
有向グラフのときには、強連結という言葉を使う。
・強連結成分分解
有向グラフを、なるべく大きい強連結な部分グラフがひとつのグループになるようにグループ分けすること。
"分解" という表現に戸惑うが、ひとつのグラフを、共通部分を持たない強連結成分たちに分解している、という立場に立つ。
ひとつのグラフをいくつかの強連結成分に分解するのであって、強連結成分をさらに細かい何らかの単位に分解するのではない。
強連結成分側の立場としては複数のノードがひとつにマージされている感覚になるので、個人的には "分解" って何やねんと思う。
どの二頂点間にもパスがあるとき、グラフは連結であるという。
孤立点があればグラフは連結ではないことになるが、「孤立点が無ければグラフは連結である」は正しいとは限らない(右図参照)。
有向グラフのときには、強連結という言葉を使う。
・強連結成分分解
有向グラフを、なるべく大きい強連結な部分グラフがひとつのグループになるようにグループ分けすること。
"分解" という表現に戸惑うが、ひとつのグラフを、共通部分を持たない強連結成分たちに分解している、という立場に立つ。
ひとつのグラフをいくつかの強連結成分に分解するのであって、強連結成分をさらに細かい何らかの単位に分解するのではない。
強連結成分側の立場としては複数のノードがひとつにマージされている感覚になるので、個人的には "分解" って何やねんと思う。
・強連結成分 (strongly connected component)
強連結成分分解でひとまとまりになるグループを強連結成分という。
強連結成分をひとつのノードにまとめる(縮約 contraction)と、グラフは DAG になる。
強連結成分分解でひとまとまりになるグループを強連結成分という。
強連結成分をひとつのノードにまとめる(縮約 contraction)と、グラフは DAG になる。
・二部グラフ (bipartite graph)
無向グラフにおいて、隣接している頂点同士が違う色になるように彩色したときに色数が $2$ なら、このグラフを二部グラフという。
一般に色数が $n$ なら、そのグラフは $n$ 部グラフ (n-partite graph) という。
・二分木 (binary tree)
根付き木の全てのノードが「子ノードの数が $2$ 以下である」という条件を満たすとき、この木を二分木という。
・橋 (bridge)
取り除くと連結成分が増える辺のことを橋という。
・間接点 (articulation point)
ある頂点と、それに接続している辺を取り除くと連結成分が増えるとき、その頂点のことを関節点という。
・union-find
グループ分けを管理するデータ構造(素集合データ構造 disjoint set)に対し、
- 要素 a と 要素 b が同じグループに含まれるのかを判定する
- 要素 a が含まれるグループと要素 b が含まれるグループをマージする
という二つの操作に名前をつけたもの。他にも以下のことができる。
- 要素 a が含まれるグループの要素数を数える
- 全部でグループがいくつあるか数える
したがって、例えば二次元グリッドの一部が塗られていて、近傍の同じ色を同一グループと見なすときに、
「グループの個数を数える」「それぞれのグループの要素数を調べる」など、幅優先/深さ優先でやりそうなことは union-find でもできる。
しかし union-find ではひとつのグループを複数に分割することはできない。
実装において、ひとつのグループはひとつの木になっている。そのため union-find木 と表現されることもある。
・全域木 (spanning tree)
ある無向グラフが連結であるとき、適当な辺を取り除いて木にしたものを全域木という。
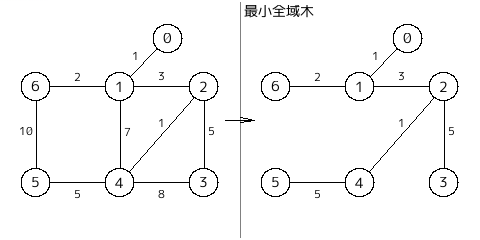
・最小全域木 (minimum spanning tree)
全域木のうち、辺のコストの総和が最小なものを最小全域木という。
アルゴリズムとして、プリム法やクラスカル法などがある。
ある無向グラフが連結であるとき、適当な辺を取り除いて木にしたものを全域木という。
・最小全域木 (minimum spanning tree)
全域木のうち、辺のコストの総和が最小なものを最小全域木という。
アルゴリズムとして、プリム法やクラスカル法などがある。
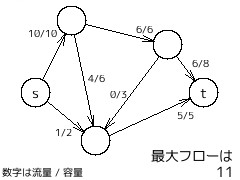
・最大流問題・最大フロー問題 (maximum flow problem)
単一始点から単一終点に向かって、いくつかの地点を経由しながらモノを流すことを考える。
地点間で流すことができる量の最大値(容量 capacity)が決まっているとする。
このとき "始点から終点に一度に流せる最大量はいくらか" を考える問題のこと。
アルゴリズムとして、Ford-Fulkerson や Dinic などがある。
始点をソース (source)、終点をシンク (sink) といい、辺の容量 (capacity) に対して実際どれだけ流れているのかを流量 (flow) という。
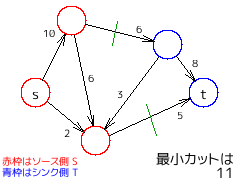
・最小カット問題 (minimum cut problem)
辺のコストが非負である有向グラフにおいて、始点から終点までのパスが存在しなくなるように辺を切ったとき、
つまり、ソースを含む頂点の集合 S とシンクを含む頂点の集合 T の二つに分割(カット cut)したとき、
S から T へ出ていく辺のコストの和を最小化する問題。※右図でコスト 3 の辺は T から S に向かっているので足さない。
最大フロー最小カット定理により、始点から終点への最大フローは始点から終点への最小カットと等しい。
そのため、最小カットを求める問題は最大フローを求めることになることがほとんどだが、
この定理に頼らないアルゴリズム (Karger の乱択 等) もあるにはある。
応用
- 複数のソースやシンクがあるとき
新たなソースとシンクを作り、新しいソースから元のソースへ最大限流出できる辺、元のシンクから新しいシンクへ最大限流出できる辺を張る。
- 無向グラフであったとき
ノード a からノード b への辺と、ノード b からノード a への辺の二本を張る。
- 頂点に容量があるとき
頂点を二つに分割し、頂点の容量で片方からもう片方に辺を張る。
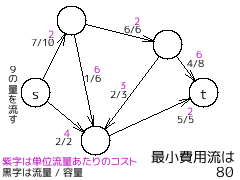
・最小費用流問題 (minimum-cost flow problem)
最大流問題のグラフにおいて、辺ごとに単位流量あたりのコストが設定されているとする。
始点から終点に向かっていくらかの量を流したとき、かかるコストの総和を最小化する問題のこと。
※右の例では $2 \times 7 + 4 \times 2 + 2 \times 6 + 6 \times 1 + 6 \times 4 + 3 \times 2 + 2 \times 5 = 80$ となる。
単一始点から単一終点に向かって、いくつかの地点を経由しながらモノを流すことを考える。
地点間で流すことができる量の最大値(容量 capacity)が決まっているとする。
このとき "始点から終点に一度に流せる最大量はいくらか" を考える問題のこと。
アルゴリズムとして、Ford-Fulkerson や Dinic などがある。
始点をソース (source)、終点をシンク (sink) といい、辺の容量 (capacity) に対して実際どれだけ流れているのかを流量 (flow) という。
・最小カット問題 (minimum cut problem)
辺のコストが非負である有向グラフにおいて、始点から終点までのパスが存在しなくなるように辺を切ったとき、
つまり、ソースを含む頂点の集合 S とシンクを含む頂点の集合 T の二つに分割(カット cut)したとき、
S から T へ出ていく辺のコストの和を最小化する問題。※右図でコスト 3 の辺は T から S に向かっているので足さない。
最大フロー最小カット定理により、始点から終点への最大フローは始点から終点への最小カットと等しい。
そのため、最小カットを求める問題は最大フローを求めることになることがほとんどだが、
この定理に頼らないアルゴリズム (Karger の乱択 等) もあるにはある。
応用
- 複数のソースやシンクがあるとき
新たなソースとシンクを作り、新しいソースから元のソースへ最大限流出できる辺、元のシンクから新しいシンクへ最大限流出できる辺を張る。
- 無向グラフであったとき
ノード a からノード b への辺と、ノード b からノード a への辺の二本を張る。
- 頂点に容量があるとき
頂点を二つに分割し、頂点の容量で片方からもう片方に辺を張る。
・最小費用流問題 (minimum-cost flow problem)
最大流問題のグラフにおいて、辺ごとに単位流量あたりのコストが設定されているとする。
始点から終点に向かっていくらかの量を流したとき、かかるコストの総和を最小化する問題のこと。
※右の例では $2 \times 7 + 4 \times 2 + 2 \times 6 + 6 \times 1 + 6 \times 4 + 3 \times 2 + 2 \times 5 = 80$ となる。
・マッチング (matching)
端点を共有しない辺の集合のことをマッチングという。
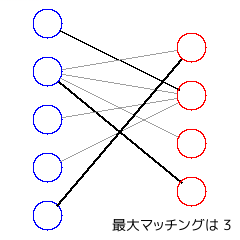
・最大マッチング (maximum matching, maximum-cardinality matching)
マッチングのうち、要素数が最大のものを最大マッチングという。
・二部マッチング (bipartite matching)
二部グラフでのマッチングを二部マッチングという。
二部グラフの最大マッチング問題は最大流問題の特殊ケースだと考えることができる。
すなわち、ソースから一色目、一色目から二色目、二色目からシンクにそれぞれ適切に辺を張って考える。
端点を共有しない辺の集合のことをマッチングという。
・最大マッチング (maximum matching, maximum-cardinality matching)
マッチングのうち、要素数が最大のものを最大マッチングという。
・二部マッチング (bipartite matching)
二部グラフでのマッチングを二部マッチングという。
二部グラフの最大マッチング問題は最大流問題の特殊ケースだと考えることができる。
すなわち、ソースから一色目、一色目から二色目、二色目からシンクにそれぞれ適切に辺を張って考える。
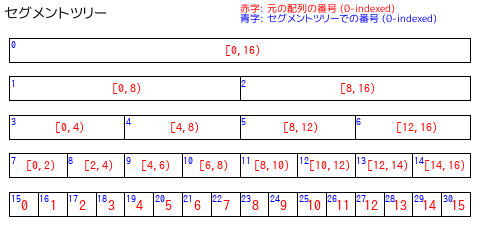
・セグメントツリー (segment tree)
区間を扱うときに重宝するデータ構造。内部的に完全二分木を実装する。
例えば、
配列におけるある範囲の最大値や最小値を求める(RMQ: Range Minimum Query)
などが得意。
右図では完全二分木を 0-indexed の一次元配列で管理している(青字の番号)。
区間を扱うときに重宝するデータ構造。内部的に完全二分木を実装する。
例えば、
配列におけるある範囲の最大値や最小値を求める(RMQ: Range Minimum Query)
などが得意。
右図では完全二分木を 0-indexed の一次元配列で管理している(青字の番号)。
(ΦωΦ)<つづく