(ΦωΦ)<グラフ理論 データの持ち方
プログラミングコンテストの場合、標準入力からデータを受け取ったり、決められたシグネチャの関数に引数として渡されるのを受け取ったりするが、グラフの問題はそれをそのまま持つのではなく、ちょっとアレンジする必要のあることが多い。
例えば、こんな有向グラフを受けとることを考える。
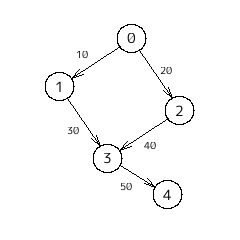
・隣接行列
#include <iostream>
#include <algorithm>
using namespace std;
int main(void) {
constexpr int inf = 987654321;
int V, E; scanf("%d%d", &V, &E); // V: 頂点の数, E: 辺の数
vector<vector<int>> G(V, vector<int>(V, inf)); // G[V][V]
for(int i=0; i<E; ++i) {
int a, b, c; scanf("%d%d%d", &a, &b, &c); // aからbにコストcで
G[a][b] = c;
}
return 0;
}
イメージ:
| from \ to | 0 | 1 | 2 | 3 | 4 |
| 0 | $\infty$ | $10$ | $20$ | $\infty$ | $\infty$ |
| 1 | $\infty$ | $\infty$ | $\infty$ | $30$ | $\infty$ |
| 2 | $\infty$ | $\infty$ | $\infty$ | $40$ | $\infty$ |
| 3 | $\infty$ | $\infty$ | $\infty$ | $\infty$ | $50$ |
| 4 | $\infty$ | $\infty$ | $\infty$ | $\infty$ | $\infty$ |
・隣接リスト
#include <iostream>
#include <algorithm>
using namespace std;
struct edge { int to, cost; };
int main(void) {
int V, E; scanf("%d%d", &V, &E); // V: 頂点の数, E: 辺の数
vector<vector<edge>> G(V, vector<edge>()); // G[V][]
for(int i=0; i<E; ++i) {
int a, b, c; scanf("%d%d%d", &a, &b, &c); // aからbにコストcで
G[a].push_back(edge({b, c}));
}
return 0;
}
イメージ:
| from \ edges | |
| 0 | [edge(to=1, cost=10), edge(to=2, cost=20)] |
| 1 | [edge(to=3, cost=30)] |
| 2 | [edge(to=3, cost=40)] |
| 3 | [edge(to=4, cost=50)] |
| 4 | [] |
辺にコストがないとき

・隣接行列
#include <iostream>
#include <algorithm>
using namespace std;
int main(void) {
int V, E; scanf("%d%d", &V, &E); // V: 頂点の数, E: 辺の数
vector<vector<bool>> G(V, vector<bool>(V, false)); // G[V][V]
for(int i=0; i<E; ++i) {
int a, b; scanf("%d%d", &a, &b); // aからbに
G[a][b] = true;
}
return 0;
}
・隣接リスト
#include <iostream>
#include <algorithm>
using namespace std;
int main(void) {
int V, E; scanf("%d%d", &V, &E); // V: 頂点の数, E: 辺の数
vector<vector<int>> G(V, vector<int>()); // G[V][]
for(int i=0; i<E; ++i) {
int a, b; scanf("%d%d", &a, &b); // aからbに
G[a].push_back(b);
}
return 0;
}
無向グラフの場合は、ノード a からノード b に辺を張るときに、ノード b からノード a にも辺を張っておく。
---
・木など、一次元配列で充分なとき
$a$ から $b$ に矢印を張る
例: $a$ の親が $b$ である
例: $a$ の親が $b$ である
G[a] = b