(ΦωΦ)＜グラフ理論対策講座

Google Code Jam Round 1C 2016 B "Slides!"

$B$ 個のノードの $1$ 番をスタート、$B$ 番をゴールとしたとき、
有向辺を辿るときのパターン数が $M$ 通りになるようなグラフを構築してください。
ただし多重辺は認められないものとします。
・$1 \le$ クエリの数 $\le 100$
・$1 \le B \le 50$
・$1 \le M \le 10^{18}$

以下 0-indexed です。
サンプルケースから、IMPOSSIBLE になるのはどんなときだろうと気になってくる。
そこで、辺を張れるだけ張ってみる。
閉路があったらその部分を何周かすればパターン数を無限に稼げるので、閉路は無いんだなというのは分かる。

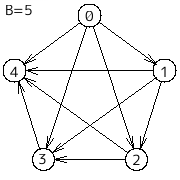
辺を張れるだけ張ると左図のようになり、パターン数は

0->             4 # 最後は 0 から 4
0->         3-> 4 # 最後は 3 から 4
0->     2->     4 # 最後は 2 から 4
0->     2-> 3-> 4 # 最後は 3 から 4
0-> 1->         4 # 最後は 1 から 4
0-> 1-> 2->     4 # 最後は 2 から 4
0-> 1->     3-> 4 # 最後は 3 から 4
0-> 1-> 2-> 3-> 4 # 最後は 3 から 4

以上 $8$ 通りになる。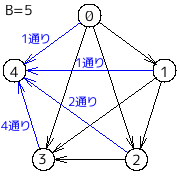

上記の内容を考察すると、
・パターン数の上限は、スタートとゴール以外のノード（中継地点と呼ぶことにする）に行くか行かないかで $2^{B-2}$ であること
・中継地点からゴールに行く最後の辺のパターン数は、$2$ の冪乗と規則的であること
が分かる（左図参照）。

パターン数 $M$ は $1$ 以上なのでスタートからゴールへの直接のルートは必ずあるようにし、
残りの $M-1$ パターンは中継地点から直接ゴールに行く辺を張るか張らないかで対応すれば答えになる。
スタートから各中継地点に行く第一歩めのパターン数で考えても良い。

#!/usr/bin/python2
# -*- coding: utf-8 -*-
# †
def f(B, M):
    relay = B - 2 # スタートとゴール以外のノード数
    if M > 2 ** relay:
        return None
    G = [[int(i < j) for j in range(B)] for i in range(B)] # G[B][B]
    for i in xrange(relay): # M-1 の右から i 番目のビットが、i+1 番のノードからゴールへの辺の有無になる
        G[i+1][B-1] = (M-1)>>i & 1
    return '\n'.join(''.join(map(str, row)) for row in G)


T = int(raw_input())
for case in xrange(T):
    line = raw_input()
    B, M = map(int, line.split())
    G = f(B, M)
    if G:
        print 'Case #{}: POSSIBLE'.format(case+1)
        print G
    else:
        print 'Case #{}: IMPOSSIBLE'.format(case+1)

---

補題

逆に、グラフが与えられたときにパターン数を求めてください。
・$1 \le B \le 50$
・ノード $u, v$ において、$u \ge v$ なら $u$ から $v$ への有向辺は無いことが保証される。

サンプルケース
入力:

出力:

※テストデータの一行目はテスト件数です。

テストデータはこちら。

// †
#include <iostream>
#include <algorithm>
using namespace std;
using i64 = long long;

int B;
vector<i64> dp;
vector<string> G;

// iからゴールへのパターン数
i64 rec(int i) {
  i64 &res = dp[i];
  if(res != -1) { return res; }
  if(i == B-1) { return res = 1; }
  res = 0;
  for(int j=i+1; j<B; ++j) {
    if(G[i][j] == '1') { res += rec(j); }
  }
  return res;
}

int main(void) {
  int T; scanf("%d", &T);
  for(int loop=0; loop<T; ++loop) {
    scanf("%d", &B);
    G.resize(B);
    for(int i=0; i<B; ++i) {
      cin >> G[i];
    }
    dp.assign(B, -1);
    i64 res = rec(0);
    printf("%lld\n", res);
  }
  return 0;
}

(ΦωΦ)＜つづく