Top
TopCoder SRM 653 Div1 Med "Singing"
$N, lo, hi$ というパラメータが与えられます。
男性は $1 \le$ 男声 $\le hi$ 、女性は $lo \le$ 女声 $\le N$ の領域の高さで声を出すことができます。
音の高さを表した楽譜が与えられます。全ての高さは男女のどちらかは必ず出せることが保証されています。
男女が入れ替わる回数を最小化したいとき、その回数を求めてください。
・$1 \le N \le 1000$
・$1 \le lo \le hi \le N$
・$1 \le$ 楽譜配列の要素数 $\le 1000$
・$1 \le$ 楽譜のそれぞれの音 $\le N$

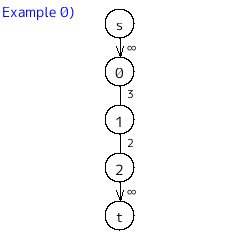
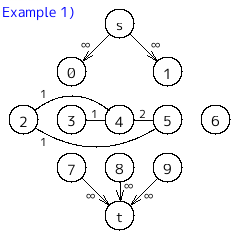
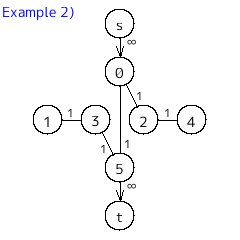
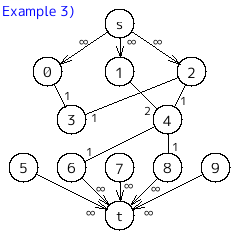
音の高さをノードにしたグラフを構築して、男声側と女声側にカットするときの最小カットが答えになるので、最大フローで考える。
始点からは男性にしか出せない音域に容量無限大で辺を張り、女性にしか出せない音域から終点に容量無限大で辺を張る。
楽譜の隣同士の音の高さを辺でつなぐが、同じ組み合わせを結ぶたびに容量をどんどん上げていく。
1-indexed が異様にめんどくさいので先に対処しておく。



#include <iostream>
#include <algorithm>
#include <queue>
using namespace std;

struct Singing { int solve(int N, int lo, int hi, vector<int> pitch); };

constexpr int inf = 987654321;

struct Edge {
  int dst, rev;
  int capa;
};

struct Graph {
  int size;
  vector<vector<Edge>> g;
  Graph(int size) : size(size) { g.resize(size); }
  void add_edge(int src, int dst, int capa);
  int max_flow(int s, int t) { throw; }
};

struct Dinic : Graph {
  vector<int> level, iter;
  Dinic(int size) : Graph(size) {}
  int max_flow(int s, int t);
private:
  void bfs(int s);
  int dfs(int v, int t, int flow);
};

void Graph::add_edge(int src, int dst, int capa) {
  g[src].push_back(Edge({dst, int(g[dst].size()),   capa}));
  g[dst].push_back(Edge({src, int(g[src].size())-1, 0}));
}

void Dinic::bfs(int s) {
  level.assign(size, -1);
  queue<int> que;
  level[s] = 0;
  que.push(s);
  while(!que.empty()) {
    int v = que.front(); que.pop();
    for(Edge& e : g[v]) {
      if(e.capa > 0 && level[e.dst] < 0) {
        level[e.dst] = level[v] + 1;
        que.push(e.dst);
      }
    }
  }
}

int Dinic::dfs(int v, int t, int flow) {
  if(v == t) { return flow; }
  for(int& i=iter[v]; i<g[v].size(); ++i) {
    Edge& e = g[v][i];
    if(e.capa <= 0 || level[v] >= level[e.dst]) { continue; }
    int d = dfs(e.dst, t, min(flow, e.capa));
    if(d > 0) {
      e.capa -= d;
      g[e.dst][e.rev].capa += d;
      return d;
    }
  }
  return 0;
}

int Dinic::max_flow(int s, int t) {
  int res = 0;
  while(true) {
    bfs(s);
    if(level[t] < 0) { return res; }
    iter.assign(size, 0);
    int flow;
    while((flow = dfs(s, t, inf)) > 0) {
      res += flow;
      if(res >= inf) { return inf; }
    }
  }
}

int Singing::
solve(int N, int lo, int hi, vector<int> pitch) {
  --lo, --hi;
  int n = pitch.size();
  for(int i=0; i<n; ++i) { --pitch[i]; }
  vector<vector<int>> G(N, vector<int>(N)); // G[N][N]
  for(int i=0; i<n-1; ++i) {
    if(pitch[i] != pitch[i+1]) {
      ++G[pitch[i]][pitch[i+1]];
      ++G[pitch[i+1]][pitch[i]];
    }
  }
  Dinic graph(N + 2);
  int s = N,
      t = N + 1;
  for(int i=0; i<lo; ++i) {
    graph.add_edge(s, i, inf);
  }
  for(int i=hi+1; i<N; ++i) {
    graph.add_edge(i, t, inf);
  }
  for(int i=0; i<N; ++i) {
    for(int j=0; j<N; ++j) {
      if(i == j) { continue; }
      if(G[i][j] == 0) { continue; }
      graph.add_edge(i, j, G[i][j]);
    }
  }
  int res = graph.max_flow(s, t);
  return res;
}

(ΦωΦ)＜つづく